Visualizando Grafos de Visibilidade
Visualizando Grafos de Visibilidade
“A série Visualizando pretende introduzir tanto conceitos conhecidos quanto novos e experimentais, através de analogias e ilustrações. Sinta-se à vontade para conversar, compartilhar e criticar conosco.”
Contexto
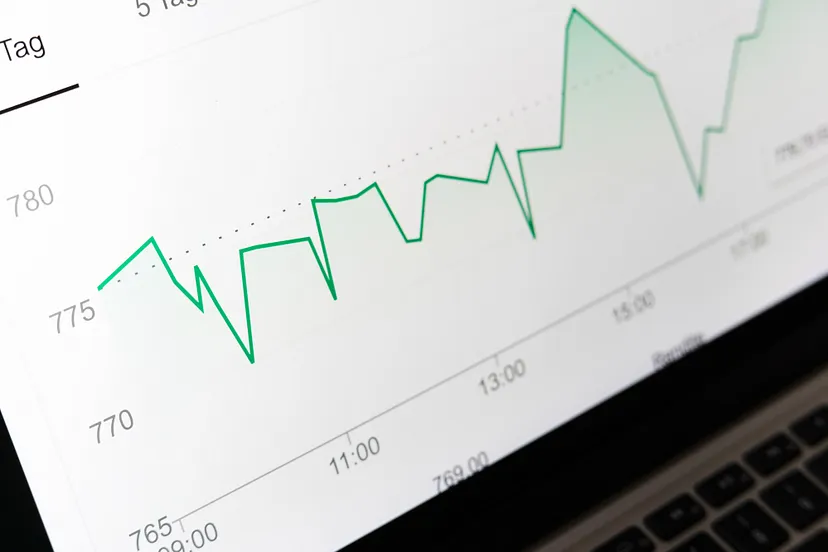
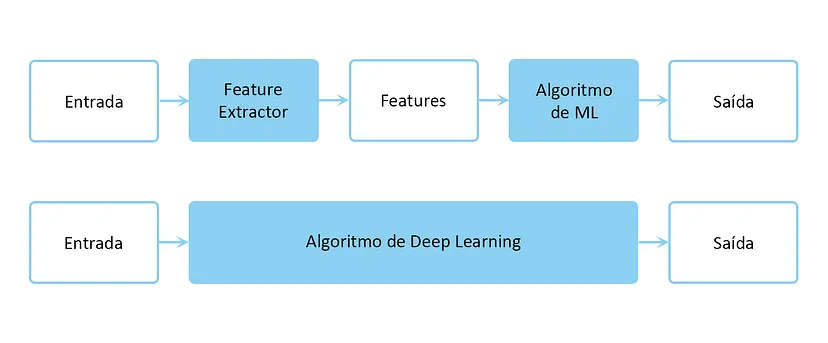
Modelos de aprendizagem profunda (vulgo deep learning) aprendem representações de um espaço durante seu processo de treinamento. Em linhas gerais um modelo aprende o que tem que enxergar, e dependendo do volume e qualidade de dados consegue executar essa tarefa muito bem.
No entanto nem sempre é necessário ou possível aplicar modelos de deep learning, seja pela baixa complexidade do problema ou pela escassez de recursos. Assim como seria um exagero usar uma britadeira para consertar uma mesa de ping pong que está se desfazendo.

Vale lembrar então que previamente (e atualmente) eram (e são) criadas handcrafted features, isto é, a criação manual de características de um objeto. Dentro do contexto de handcrafted features se situam os grafos de visibilidade, como uma forma diferente de enxergar séries temporais através da ótica da teoria de grafos e de redes complexas para então extrair informações valiosas.
Na prática esse é um conceito super simples e novo que eu espero que tenha maior aplicação no futuro, mas como tudo que é pesquisa e desenvolvimento, pode cair no esquecimento. Ainda assim, espero que seja uma forma interessante de evidenciar a importância do esquecimento.
Aliás, recomendo a leitura dos posts sobre carreira do professor Terence Tao. Em específico este, em que trata das etapas de educação matemática e da importância da intuição, fator essencial para pesquisa e desenvolvimento.
Note que o enfoque em grafos de visibilidade pode ser também puramente matemático, em que eu em particular creio que tem melhor futuro.
Grafos de Visibilidade
Imagine você em um universo que apenas existem arranha-céus e gostaria de ver outro arranha-céu. Regresse também para aulas de física do ensino médio, do tempo em que pinguins podiam ser aproximados por esferas, e aproxime então todos os prédios por paralelepípedos com alturas diferentes.

Dadas essas restrições, você percebe que consegue enxergar outro prédio (ou o topo do prédio) apenas caso não existam prédios intermediários que bloqueiem a visão. Isto é, você tem visibilidade de outro prédio apenas caso possa traçar uma reta de visão que não intercepte outro prédio.
Isolando cada vez mais nosso universo, imagine também que estamos limitados ao lado de uma avenida. Nesse momento eu começo a me perguntar “Como eu fui cair nesse universo melancólico mesmo?” Até curtiria adicionar menções a O Gambito da Rainha, mas não vai ser desta vez.
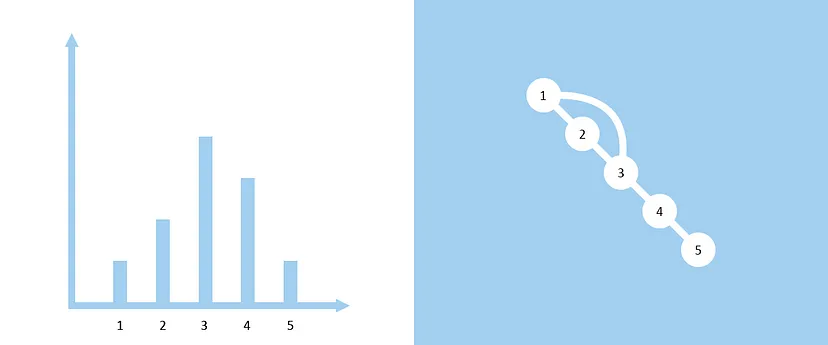
Então confinados apenas ao lado de uma avenida (seria esse um cenário primo de flatland) e com visibilidade apenas da esquerda e direita, não seria esquisito alguém confundir o cenário com uma gráfico de barras de uma série temporal (admito que foi meio forçado). No entanto seria improvável, mas por falta de criatividade essa é a analogia. Aguente mais um pouco por favor.
Agora imagine que cada prédio (barra, como desejar) represente um vértice e a visibilidade entre dois prédios represente a aresta entre dois vértices, logo temos um grafo de visibilidade relacionado a uma série temporal.
Código
Para criação de grafo de visibilidade a partir de uma série temporal vamos aplicar o algoritmo sort and conquer proposto por Ghosh et al [4]. Este algoritmo é dividido em dois módulos, o modulo de visibilidade que efetivamente anota o que é visível, isto é, cria as arestas do grafo; e o módulo principal, responsável por controlar o processo.
Seu módulo de visibilidade age de forma iterativa em cada um dos vértices. Para um vértice particular anotamos os demais vértices que temos visibilidade, isto é, que não estão ocultos por um vértice anterior dado um tamanho de vizinhança máximo.
De forma específica, para vértices a direita do vértice atual i comparo a inclinação entre dois vértices atuais a maior inclinação anterior (linha 20). Caso a inclinação atual seja maior, então atualizo a maior inclinação (linha 21) e adiciono esta aresta (linha 22 e 23). Caso contrário, então não tenho visibilidade deste vértice. Processo análogo para os vértices à esquerda.
def wvisibility(x, left, right, i, graph):
'''Weighted visibility module of sort and conquer algorithm proposed by Ghosh et al.
Parameters:
x: numpy.array
A 1d time series.
left: int
Leftmost node connected to current node.
right: int
Rightmost node connected to current node.
i: int
Current node.
graph: scipy.sparse.lil.lil_matrix
A graph in row-based list of lists format.
'''
max_slope = float('-inf')
min_slope = float('+inf')
for j in np.arange(i + 1, right):
slope = (x[j] - x[i]) / (j - i)
if slope > max_slope:
max_slope = slope
graph[i, j] = np.arctan(slope)
graph[j, i] = np.arctan(slope)
for j in np.arange(i - 1, left, -1):
slope = (x[i] - x[j]) / (i - j)
if slope < min_slope:
min_slope = slope
graph[i, j] = np.arctan(slope)
graph[j, i] = np.arctan(slope)Módulo de visibilidade do algoritmo sort and conquer.
Então o módulo sort and conquer atua priorizando a aplicação do módulo de visibilidade, escolhendo primeiramente os maiores vértices (linha 9). Desta forma, implicitamente criamos limitações de vizinhança para os demais vértices não visitados (linha 21). Isto é, do arranha-céu conseguimos medir que um prédio é maior do que outro, desta forma sabemos que de um prédio current não é possível enxergar além do prédio left a sua esquerda (linha 18) ou do prédio right a sua direita (linha 20). Essas informações se encontram codificadas nas arestas previamente formadas.
def sort_and_conquer(x):
'''Sort and conquer algorithm proposed by Ghosh et al.
Parameters:
x: numpy.array
A 1d time series.
'''
n = x.size
sortd = np.argsort(x)[::-1]
graph = sparse.lil_matrix((n, n))
for i in np.arange(n):
current = sortd[i]
connected = graph.rows[current]
left = -1
right = n
for j in connected:
if j < current:
left = max(left, j)
else:
right = min(right, j)
wvisibility(x, left, right, current, graph)
return sparse.csr_matrix(graph)Módulo principal do algoritmo sort and conquer.
Aplicações
Dada uma série temporal, primeiramente representamos a mesma como grafo de visibilidade. Em seguida podemos: 1) Usar sua sequência ou distribuição de graus como handcrafted feature; ou 2) Explorar sua distribuição de graus.
A primeira opção é simples, e através de curtos snippets conseguimos extrair características em que podemos aplicar um algoritmo de machine learning tradicional, como knn ou support vector machine.
def get_degree_sequence(graph):
'''Get a degree sequence of a graph.
Parameters:
graph: scipy.sparse.csr.csr_matrix
A graph in compressed sparse row format.
'''
degree_seq = graph.sum(axis=0).A.ravel()
return degree_seqExtração de uma sequência de graus de uma matriz de adjacência.
def get_degree_distribution(degseq):
'''Get a degree distribution of a graph.
Parameters:
degseq: numpy.ndarray
A sequence of degrees.
'''
degree, frequency = np.unique(degseq, return_counts=True)
distribution = frequency / frequency.sum()
return distributionExtração de uma distribuição de graus de uma sequência de graus.
Caso queira se aprofundar mais, disponibilizo um código que realiza a transformação de uma série temporal para sequência de graus de seu respectivo grafo de visibilidade. Note que este é um caso em que a transformação não resultou em melhora na classificação.
Já a segunda opção, de explorar a relação entre uma série temporal e sua distribuição de graus do grafo de visibilidade, apresenta maior beleza e complexidade e portanto será abordada em futuros posts.
Observações
Obrigado por me acompanhar até aqui, boa semana!!
Referências
[1] Lacasa, Lucas et al. “From time series to complex networks: The visibility graph”. Em: Proceedings of the National Academy of Sciences 105.13 (2008), pp. 4972–4975.
[2] Ghosh, Saptorshi e Dutta, Amlan. “An efficient non-recursive algorithm for transforming time series to visibility graph”. Em: Physica A: Statistical Mechanics and its Applications 514 (2019), pp. 189–202.